처음 인수분해를 접할 때, 대수막대를 이용하면 편리하다. 전개된 이차식에서 \( x^2\) , \( x\)의 일차항, 그리고 상수항이 있다고 할 때, \( x^2\)은 정사각형으로, \( x\)은 한 변의 길이가 1이고 다른 변의 길이가 \( x\) 인 직사각형, 그리고 한 변의 길이가 1인 정사각형을 가지고 표현하는 것이다.


다항식을 대수 막대로 표현하기
곱셈공식의 전개된 식은 다항식으로 이루어져 있다. 위의 그림처럼 대수막대를 도형으로 나타낼 수 있다. 보라색 정사각형은 한 변의 길이가 x이기 때문에 \( x^2 \) 로 표현된다. 연두색 직사각형은 \(x\) 으로 표현할 수 있다. 가로와 세로 모두 1인 정사각형은 상수항으로 표현된다.
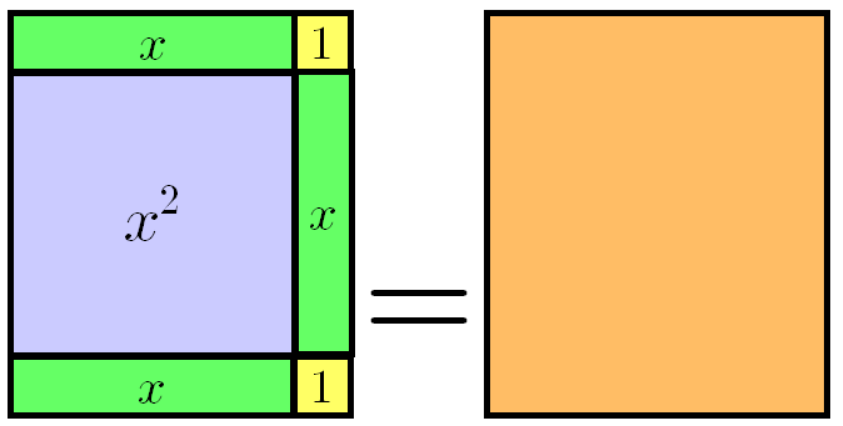
직사각형의 넓이 구하기
위의 모습의 대수막대를 다항식으로 표현하면, \( x^2 + 3x+2 \) 라고 표현된다. 왼쪽 그림을 보고 오른쪽 전체 직사각형의 넓이를 구한다면 가로와 세로의 길이는 어떻게 알 수 있을까?
그렇다. 왼쪽의 그림에서 개수로 연두색 직사각형의 개수가 \( x\)의 계수(변수(문자)에 곱해진 상수(숫자)) 역할을 하게 된다.
따라서, 오른쪽의 큰 직사각형의 가로와 세로의 길이는 왼쪽 대수 막대를 보고 구할 수 있다. 위의 그림을 식으로 나타내면 다음과 같다.
$$ x^2 + 3x + 2 = (x+1 ) (x+2) $$
왼쪽에서 오른쪽으로 풀 때는 '인수분해'라고 하고 반대인 경우는 '전개한다.' 라고 한다.
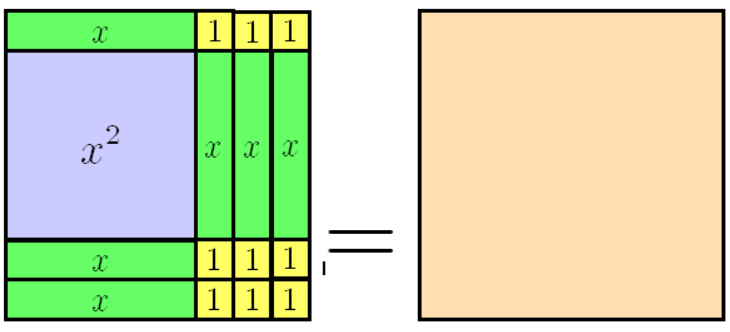
정사각형 넓이로도 변하는 경우
바로 완전제곱식이다. 앞서서도 포스팅한 것과 마찬가지로 정사각형의 넓이를 알고, 한 변의 길이를 \(x\)라고 한다면 \(x^2 = 상수\)로 표현된다. 곱셈공식에서는 가로와 세로의 길이를 늘려서 가로와 세로의 곱으로 표현하여 전개하였다면, 이번에는 전개된 식에서 가로와 세로를 다시 구하는 작업이다.
$$ x^2 + 6x + 9 = (x+3)^2 $$
마찬가지로 좌변과 우변의 식을 쓸 수 있다. 대수막대를 이용하여 써 봤을 때, 직사각형이 아닌 정사각형임을 알 수 있다.
이 활동으로 알아야 하는 것은
곱셈식을 인수분해 할 수 있다는 사실이다. 전개되어서 단항식의 덧셈으로 이루어진 다항식을 다항식의 곱으로 나타낼 수 있다. 곱셈공식이라고 외워야 하는 것은 아니다. 중학교에서 나오는 두 일차식의 곱을 '전개'하는 것과 전개된 이차식을 일차식의 곱으로 나타낼 수 있으면 된다. 이처럼 넓이를 이용해서 이차식을 이해하는 것은 나중에 미분과 적분에서도 큰 잇점이 된다. 따라서 도형을 식으로 나타낼 수 있도록 많이 연습해두면 좋다.
'개념수학' 카테고리의 다른 글
| 초등학교 3학년 2학기 곱셈과 나눗셈 (0) | 2022.09.14 |
|---|---|
| 초6 2학기 분수의 나눗셈 교과서의 설명 (0) | 2022.09.14 |
| 기초학력미달학생이 수학을 잘 하기 위한 방법 (0) | 2022.09.05 |
| 유아의 수 세기 능력 발달 (0) | 2022.09.05 |
| 유아의 수 개념 획득에 대한 피아제와 겔만의 관점과 겔만의 수세기 원리 (0) | 2022.09.05 |




댓글